• Linear Combination
• Span
• How many solutions?

Linear Combination

• Give a victor set \{u_1,u_2,...,u_k\}
• The linear combination of the vectors in the set:
  • v=c_1u_1+c_2u_2+...+c_ku_k
  • c_1,c_2,...,c_k are scalars(Cofficients of linear combination)

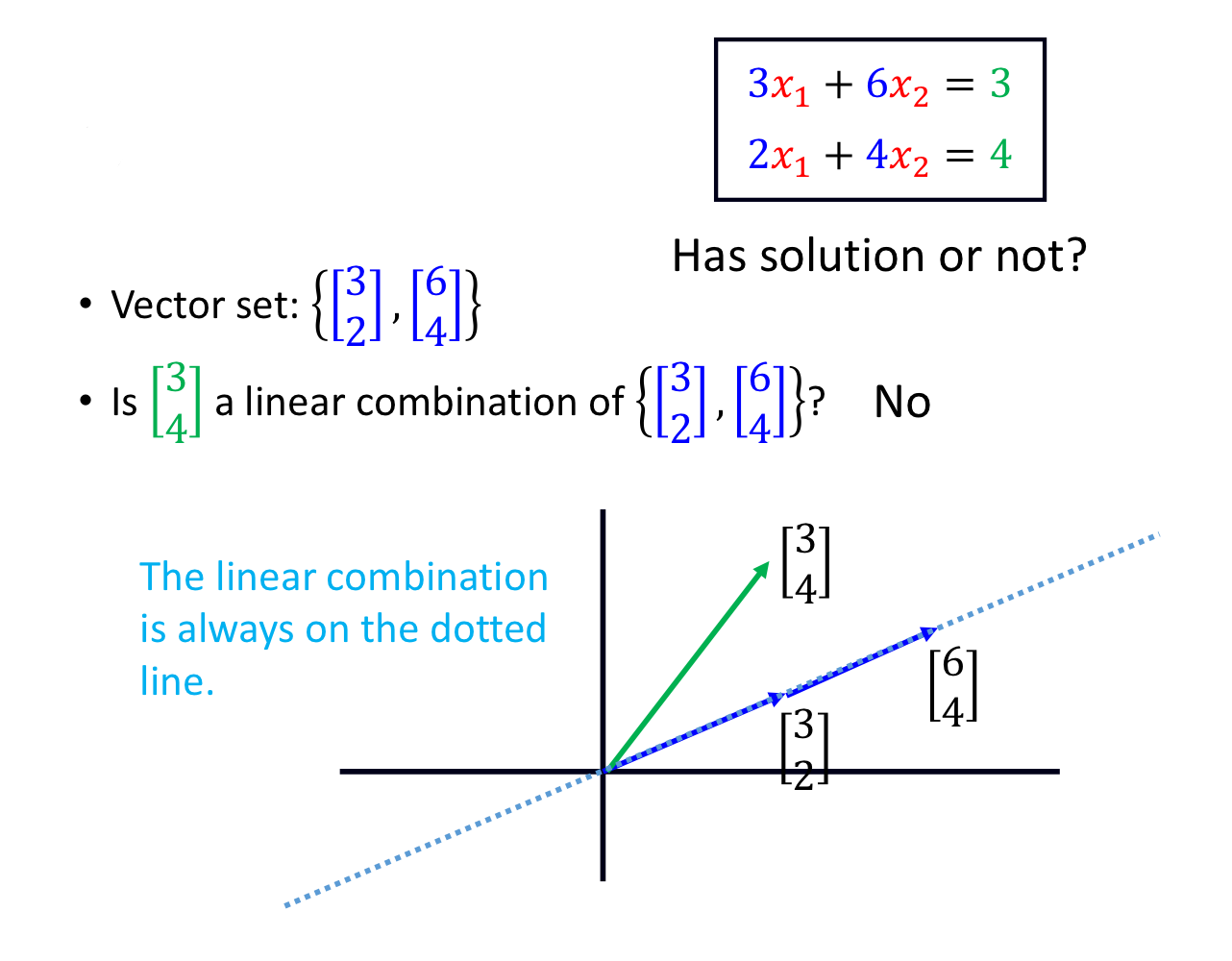
Have solution or not?
= Is b the linear combination of columns of A?

Span

• Span is the vector set of all linear combinations.

How many solutions?

• The columns of A are idependent.

  • Rank A = n
  • Nulliity = 0
  • Unique solution

• The columns of A are dependent.

  • Rank A < n
  • Nullity A > 0
  • Infinite solution

• A set of vector\{a_1,a_2,...,a_n\} is linear dependent

  • if there exist scalars x_1,x_2,...,x_n not all zero, such shat

x_1