从网络图的邻阶矩阵(0、1矩阵,0代表指标间没有边,1代表指标间有边)中删除节点并求剩余矩阵“特征值”被用来表征网络抗毁性,该方法被用在比较不同组的微生物共现网络图的稳定性中。用法为:删除网络图中的1、2、3、4、5、6、7、......N个节点并求取每次删后矩阵的特征值并做转化,将最终结果称为自然连通度。在实际中,一个网络图包含多个节点,那么如何使得某次删除的节点具有代表性呢?一种方法是根据节点的Degree大小来排序,Degree从大到小依次删除节点并计算剩余节点的邻接矩阵的自然连通度。然而,当网络图中的大部分节点的Degree比较接近甚至相等时,按照Degree排序删除节点的做法将不再有效。实施上,我们可以近似认为用删除节点的方式是模拟环境变化使得群落中某些物种消失(或某些物种之间的关系消失,即删除边)之后评估群落的稳定性如何。那么,我们事先不知道哪些物种会消失,例如,当群落中的N个物种消失时,我们很难知道这些N个物种的组合里具体是哪些物种,因此我们使用随机抽样的方法对节点进行随机抓取并删除的方法来模拟物种的随机消失,即计算随机抓取N个节点并删除之后的自然连通度。为了提高结果的可重复性,我们设定删除N个节点时可以迭代1000次(甚至更多次)并分别计算每次删除之后的自然连通度,最后取均值。当网络图节点数目大时,邻接矩阵特征值的计算量非常大,我们在实际计算过程中发现,当删除N个节点时,其自然连通度与(N-1)和(N+1)的结果很接近,因此,在尽量不改变原始结果的情况下,我们设定了步长(step)。当步长大于1,假设为3,那么删除的节点数将为1、4、7、10......(N+step),在这种设置下,计算所需时间将比原始数据(步长为1)至少减少3倍。
图片alt
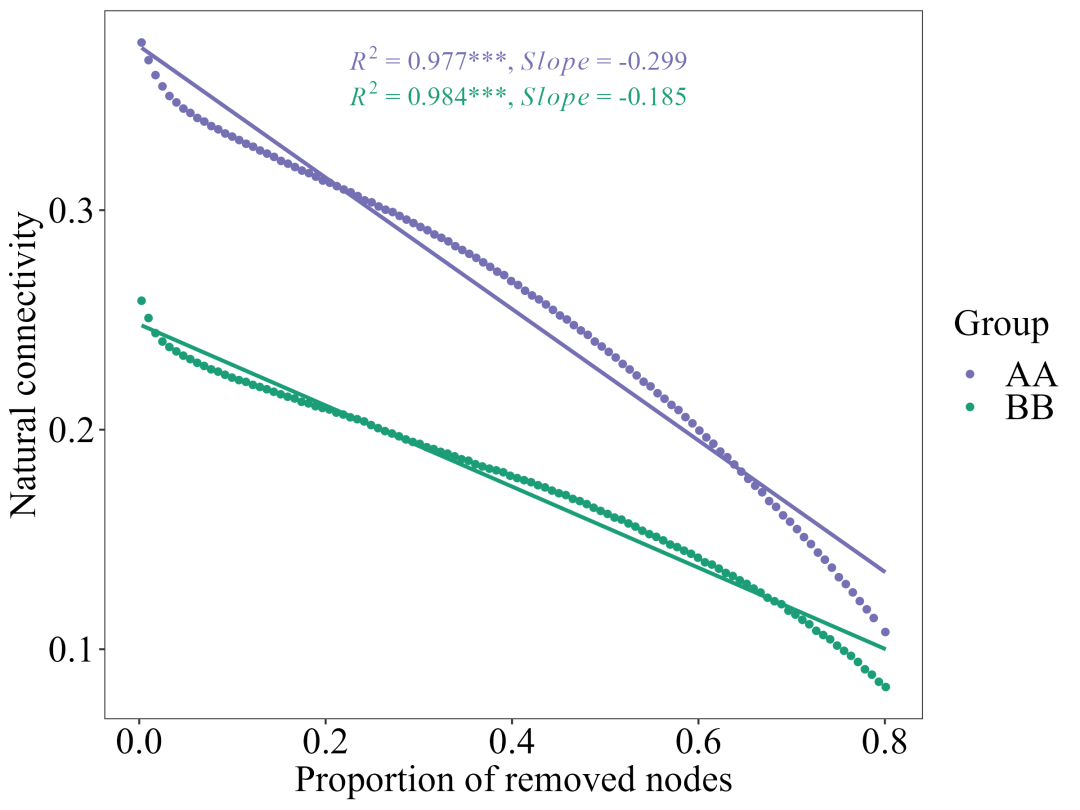
从上图可知,AA组自然连通度下降趋势快于BB组