方差分析主要用于多个样本均数比较的假设检验,因为当我们使用t检验进行多组样本间均数的假设检验时,常常会增加一类错误。
方差分析的主要思想是分解变异,即将总变异分解为处理因素引起的变异和随机误差引起的变异,通过对两者进行比较做出处理因素有无作用的统计推断。
library(rstatix)
library(tidyverse)
expr <- tibble(gene=c(sample(rnorm(1000,mean = 5,sd = 5),10,replace = T),
sample(rnorm(1000,mean = 5,sd = 5),10,replace = T),
sample(rnorm(1000,mean = 5,sd = 5),10,replace = T)),
group=factor( c(rep("treat1",10),rep("treat2",10),rep("treat3",10)) ))
head(expr)
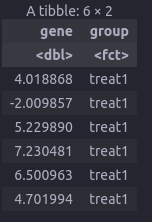
图片alt
anova_test(expr,gene ~ group)
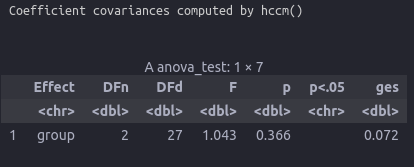
图片alt
fit <- aov(gene ~ group, data=expr)
summary(fit)
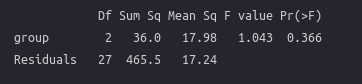
图片alt
treat1 <- expr$gene[expr$group=="treat1"]
treat2 <- expr$gene[expr$group=="treat2"]
treat3 <- expr$gene[expr$group=="treat3"]
all <- c(treat1,treat2,treat3)
SST <- sum( ( all- mean(all) )^2 )
# SST
SSE <- sum( ( treat1 - mean(treat1) )^2 ) + sum( ( treat2 - mean(treat2) )^2 ) + sum( ( treat3 - mean(treat3) )^2 )
# SSE
MSE <- sse/ (3*(10-1))
# MSE
SSt <- SST-SSE
# SSt
MSt <- SSt/(3-1)
# MSt
( ( mean(treat1) - mean(all) )^2 +( mean(treat2) - mean(all) )^2 + ( mean(treat3) - mean(all) )^2 )/2 * 10
tribble(~SS,~df,~MS,~F,~P,
SSt,(3-1),SSt/(3-1), ( SSt/(3-1) )/( SSE/( 3*(10-1) ) ), pf(1.043246, 2, 27, lower.tail = FALSE, log.p = FALSE), # 单侧右尾
SSE,3*(10-1),SSE/( 3*(10-1) ),NA,NA,
SST,3*10-1,NA,NA,NA
)
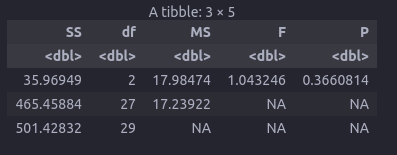
图片alt
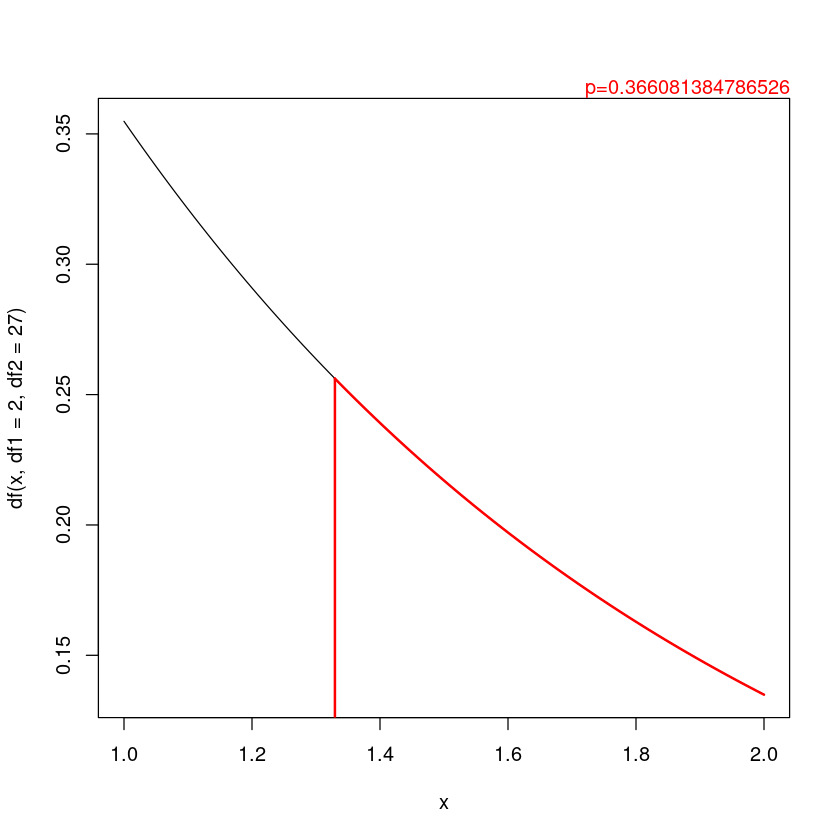
curve(df(x,df1 = 2,df2 = 27),from = 1,to = 2)
curve(df(x,df1 = 2,df2 = 27), from = 1.329567,to = 2,add = TRUE, col = "red", lwd = 2)
# abline(v=1.329567,col="red")
segments(1.329567,0,1.329567,df(1.329567,df1 = 2,df2 = 27),lwd=2,col='red')
df(1.329567,df1 = 2,df2 = 27)
# mtext("dnorm(x, log=TRUE)", adj = 0)
mtext(paste0("p=",pf(1.043246, 2, 27, lower.tail = FALSE, log.p = FALSE)), col = "red", adj = 1)
图片alt