t-distributed stochastic neighbor embedding (t-SNE) is a statistical method for **visualizing high-dimensional data **by giving each datapoint a location in a two or three-dimensional map.
SNE(stochastic neighbor embedding )
Gaussion distribution

图片alt
Stochastic Neighbor Embedding (SNE) starts by converting the high-dimensional Euclidean distances between datapoints into conditional probabilities that represent similarities.
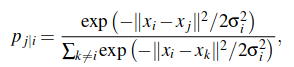
图片alt
i点出现时,出现j点的概率,这里用于描述i点和j点之间的位置关系,当x_i与x_j的距离比较近时p_{j|i}的值比较大
For the low-dimensional counterparts y_i and y_j of the high-dimensional datapoints x_i and x_j, it ispossible to compute a similar conditional probability, which we denote by q_{j|i}
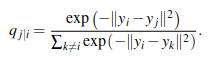
图片alt
方差固定的高斯分布
Kullback–Leibler divergence,also called relative entropy and I-divergence, denoted D_{KL}(P||Q) is a type of statistical distance: a measure of how one probability distribution P is different from a second, reference probability distribution Q. In the simple case, a relative entropy of 0 indicates that the two distributions in question have identical quantities of information.
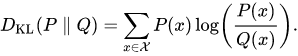
图片alt
SNE aims to find alow-dimensional data representation that minimizes the mismatch between p_{j|i} and q_{j|i}. A natural measure of the faithfulness with which q_{j|i} models p_{j|i} is the Kullback-Leibler divergence.
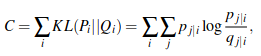
图片alt
利用KL-divergen衡量两个分布之间的差异
SNE minimizes the sum of Kullback-Leibler divergences over all datapoints using a gradient descent method.
t-Distributed Stochastic Neighbor Embedding
Symmetric SNE

图片alt
The Crowding Problem

图片alt
当高维空间的点距离比较近时,如上图中p_{ij}的值比较大,当映射到低维空间时, p_{ij}将变的更大。
当高维空间的点距离比较远时,如上图中q_{ij}的值比较小,当映射到低维空间时, q_{ij}将变的更大。
t-SEN 步骤

图片alt

图片alt