R代码实现
Getting started
library(survival)
?lung
- time: Survival time in days
- status: censoring status 1=censored, 2=dead
Survival Curves
The status indicator, normally 0=alive, 1=dead.
Other choices are TRUE/FALSE (TRUE = death) or 1/2 (2=death).
For interval censored data, the status indicator is 0=right censored, 1=event at time, 2=left censored, 3=interval censored. For multiple endpoint data the event variable will be a factor, whose first level is treated as censoring. Although unusual, the event indicator can be omitted, in which case all subjects are assumed to have an event.
s <- Surv(lung$time, lung$status)
sfit <- survfit(Surv(time, status)~1, data=lung)
summary(sfit)
Call: survfit(formula = Surv(time, status) ~ 1, data = lung)
time n.risk n.event survival std.err lower 95% CI upper 95% CI
5 228 1 0.9956 0.00438 0.9871 1.000
11 227 3 0.9825 0.00869 0.9656 1.000
12 224 1 0.9781 0.00970 0.9592 0.997
13 223 2 0.9693 0.01142 0.9472 0.992
15 221 1 0.9649 0.01219 0.9413 0.989
26 220 1 0.9605 0.01290 0.9356 0.986
30 219 1 0.9561 0.01356 0.9299 0.983
31 218 1 0.9518 0.01419 0.9243 0.980
53 217 2 0.9430 0.01536 0.9134 0.974
54 215 1 0.9386 0.01590 0.9079 0.970
sfit <- survfit(Surv(time, status)~sex, data=lung)
summary(sfit, times=seq(0, 1000, 100))
Call: survfit(formula = Surv(time, status) ~ sex, data = lung)
sex=1
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0 138 0 1.0000 0.0000 1.0000 1.000
100 114 24 0.8261 0.0323 0.7652 0.892
200 78 30 0.6073 0.0417 0.5309 0.695
300 49 20 0.4411 0.0439 0.3629 0.536
400 31 15 0.2977 0.0425 0.2250 0.394
500 20 7 0.2232 0.0402 0.1569 0.318
600 13 7 0.1451 0.0353 0.0900 0.234
700 8 5 0.0893 0.0293 0.0470 0.170
800 6 2 0.0670 0.0259 0.0314 0.143
900 2 2 0.0357 0.0216 0.0109 0.117
1000 2 0 0.0357 0.0216 0.0109 0.117
sex=2
time n.risk n.event survival std.err lower 95% CI upper 95% CI
0 90 0 1.0000 0.0000 1.0000 1.000
100 82 7 0.9221 0.0283 0.8683 0.979
200 66 11 0.7946 0.0432 0.7142 0.884
300 43 9 0.6742 0.0523 0.5791 0.785
400 26 10 0.5089 0.0603 0.4035 0.642
500 21 5 0.4110 0.0626 0.3050 0.554
600 11 3 0.3433 0.0634 0.2390 0.493
700 8 3 0.2496 0.0652 0.1496 0.417
800 2 5 0.0832 0.0499 0.0257 0.270
900 1 0 0.0832 0.0499 0.0257 0.270
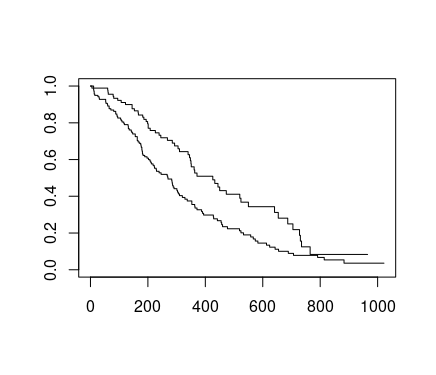
From these tables we can start to see that males tend to have worse survival than females.
plot(sfit)
?plot.survfit
图片alt
library(survminer)
ggsurvplot(sfit)

图片alt
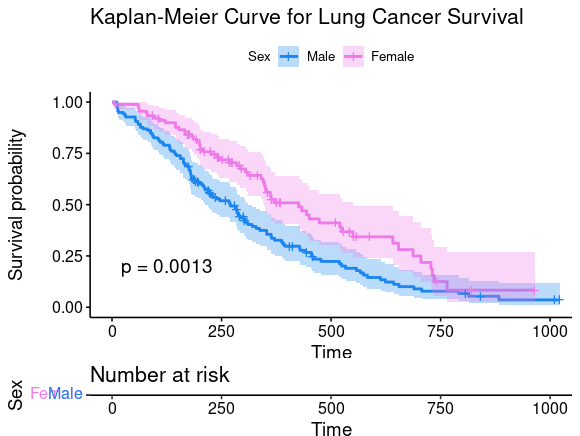
ggsurvplot(sfit, conf.int=TRUE, pval=TRUE, risk.table=TRUE,
legend.labs=c("Male", "Female"), legend.title="Sex",
palette=c("dodgerblue2", "orchid2"),
title="Kaplan-Meier Curve for Lung Cancer Survival",
risk.table.height=.15)
图片alt
Let’s add confidence intervals, show the p-value for the log-rank test, show a risk table below the plot, and change the colors and the group labels.
diff <- survdiff(formula,data = expr)
pVal <- 1 -pchisq(diff$chisq,df =1)
pValue <- signif(pVal,4)
正规化Cox回归
glmnet使用Breslow approximation处理生存时间的关系。这与survival package’s coxph函数不同,后者的默认tie-handling method是Efron approximation。
# create x matrix
set.seed(1)
nobs <- 100; nvars <- 15
x <- matrix(rnorm(nobs * nvars), nrow = nobs)
# create response
ty <- rep(rexp(nobs / 5), each = 5)
tcens <- rbinom(n = nobs, prob = 0.3, size = 1)
y <- Surv(ty, tcens)
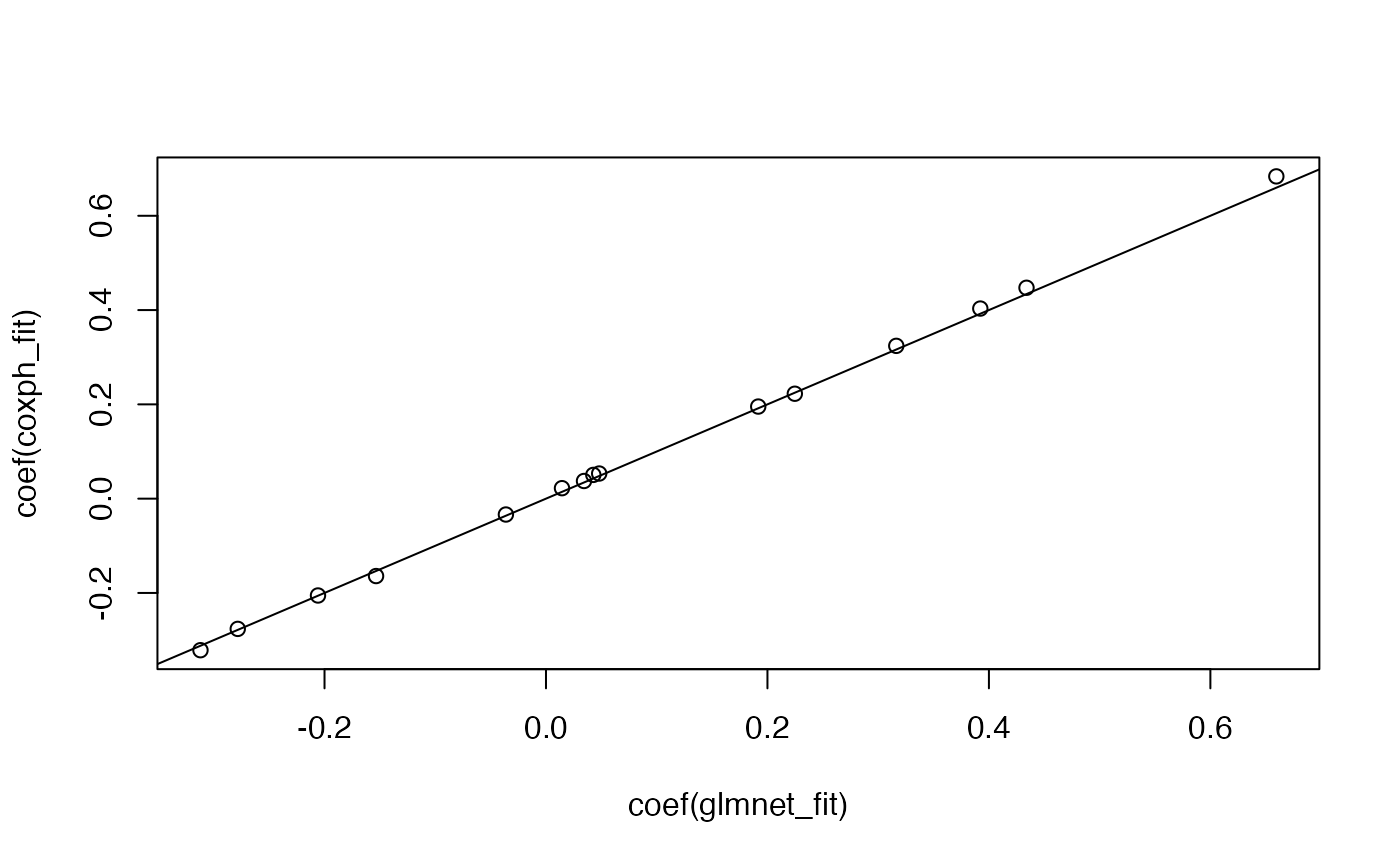
# coefficients from these two models will not line up because
# of different tie handling methods
glmnet_fit <- glmnet(x, y, family = "cox", lambda = 0)
coxph_fit <- coxph(y ~ x)
plot(coef(glmnet_fit), coef(coxph_fit))
abline(0, 1)
> coxph_fit
Call:
coxph(formula = y ~ x)
coef exp(coef) se(coef) z p
x1 0.05039 1.05169 0.21966 0.229 0.81854
x2 -0.16417 0.84860 0.20029 -0.820 0.41240
x3 0.44732 1.56412 0.19542 2.289 0.02208
x4 -0.32146 0.72509 0.21657 -1.484 0.13773
x5 -0.03365 0.96691 0.13810 -0.244 0.80751
x6 0.19536 1.21574 0.20934 0.933 0.35073
x7 0.22255 1.24926 0.18222 1.221 0.22197
x8 -0.20540 0.81432 0.19706 -1.042 0.29725
x9 0.05330 1.05475 0.24046 0.222 0.82456
x10 0.40321 1.49663 0.20686 1.949 0.05127
x11 0.32410 1.38279 0.20433 1.586 0.11270
x12 0.02223 1.02248 0.20695 0.107 0.91447
x13 -0.27625 0.75863 0.19000 -1.454 0.14596
x14 0.03746 1.03817 0.26100 0.144 0.88588
x15 0.68355 1.98089 0.23627 2.893 0.00381
Likelihood ratio test=21.55 on 15 df, p=0.1202
n= 100, number of events= 33
> glmnet_fit
Call: glmnet(x = x, y = y, family = "cox", lambda = 0)
Df %Dev Lambda
1 15 10.39 0
图片alt
glmnet目前无法执行
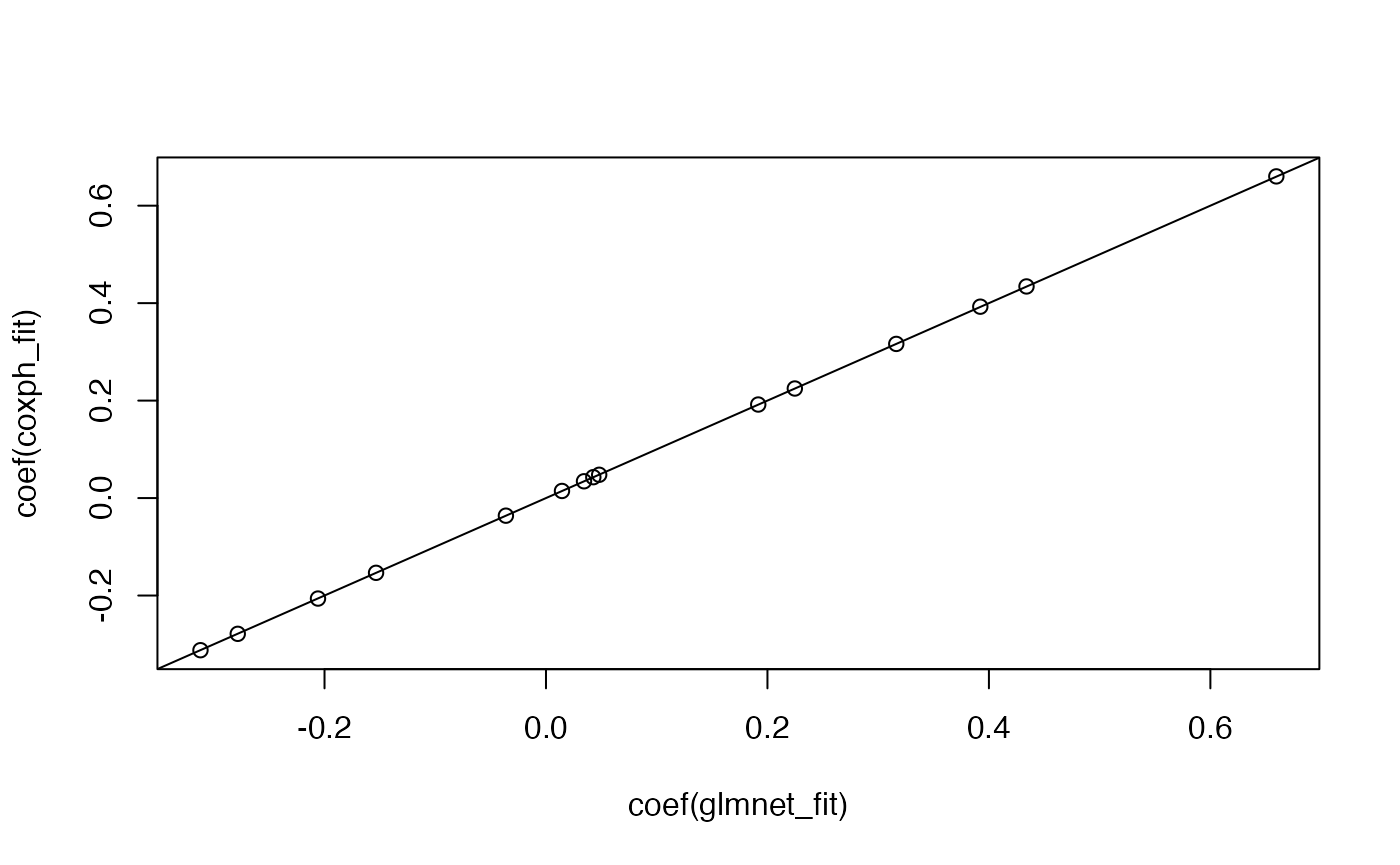
Efron approximation。survival的coxph可以通过指定ties = "breslow"来执行Breslow approximation:
# coefficients from these two models will line up
glmnet_fit <- glmnet(x, y, family = "cox", lambda = 0)
coxph_fit <- coxph(y ~ x, ties = "breslow")
plot(coef(glmnet_fit), coef(coxph_fit))
abline(0, 1)
图片alt
ggrisk 高效绘制风险因子联动图
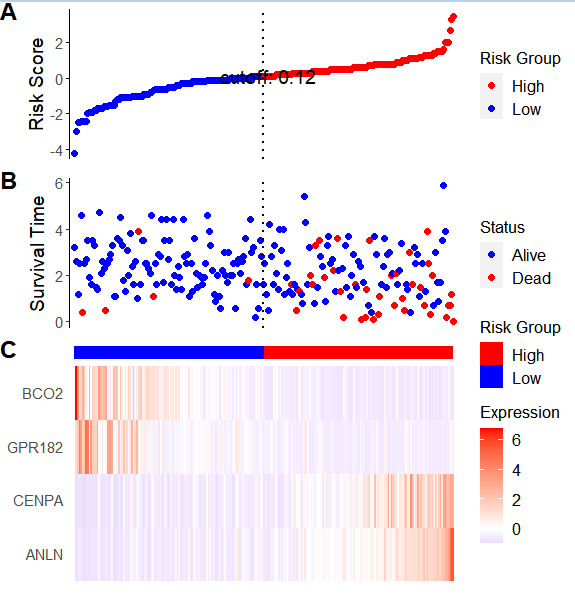
图片alt
常见问题
- Time variable is not numeric
- Invalid status value, must be logical or numeric
mutate(Overall_Survival_Status = as.numeric(Overall_Survival_Status),
days_to_last_followup=as.numeric(days_to_last_followup))